Note
Click here to download the full example code
Bauphysik¶
Formeln für Bauphysikalische Berechnungen
1 Randbedingungen (Klima)¶
A1.1 gleitenden Mittelwerts der Aussentemperatur¶
Die Komfort-Anforderungen an die empfundene Temperatur werden in der Norm SIA 180:2014 [1.4] neu in Abhängigkeit des gleitenden Mittelwerts der Aussentemperatur θrm über 48 Stunden gemäss folgender Formel festgelegt.
\(\theta_{rm}(t) = \frac{ 1 }{ N } * \sum_{j=0}^{N-1} \theta_e(t-j)\)
- gleitender Mittelwert der Aussentemperatur fiir die Stunde t
- Aussenlufttemperatur der Stunde t-j
- N Anzahl in den Mittelwert einbezogener Stunden N=48
A1.2 maximale Luftgeschwindigkeit¶
\(V_{max} = 0.54 * (\frac{g* \Delta T}{T_i})^{0.5} * H^{0.5}\)
\(V_{max} = k * \sqrt{\Delta \theta * H}\)
- Temperaturdifferenz zwischen Raumluft und kalter Oberflache
- Höhe der vertikalen Flache
- Regressionskoeffizient I
A1.1
# A1.2
def max_air_flow_speed(delta_temp, air_temperature, height):
"""Vmax = m*s^-1"""
GRAV = 9.81
return 0.54 * (GRAV * delta_temp / air_temperature) ** 0.5 * height**0.5
print(max_air_flow_speed.__doc__)
print(max_air_flow_speed(10, 20, 1))
Out:
Vmax = m*s^-1
1.1959506678789056
2 Wärme¶
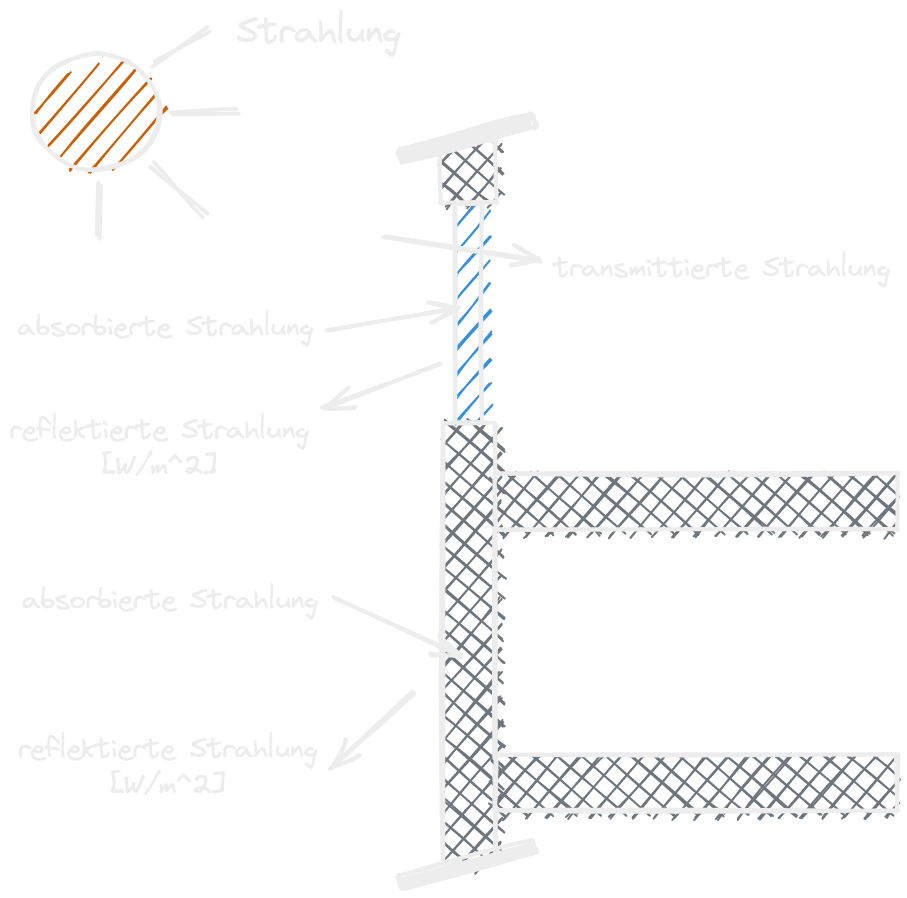
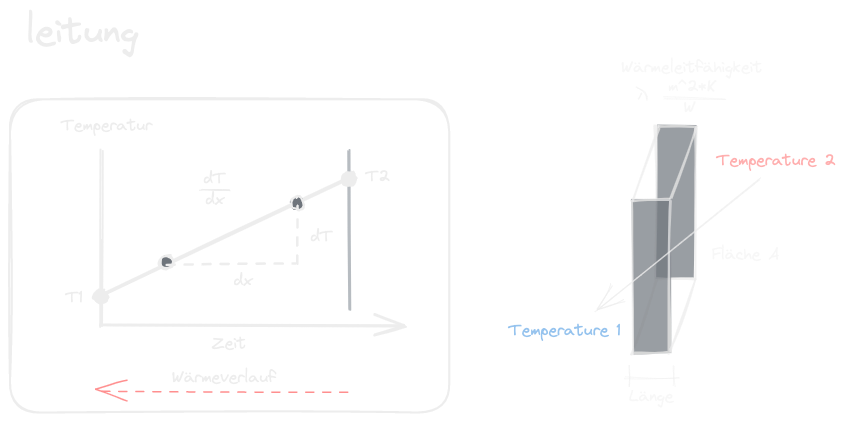
docs/generated/gallery/images/wärme_konvektion.excalidraw.png
A2.1 Wärmestromdichte q [\(W/m^{2}\)]¶
\(q = h_c * (\theta_s - \theta_a) + h_r * (\theta_s - \theta_r)\)
- \(q\) Warmestromdichte \(W/m^{2}\)
- \(h_c\) Warmeiibergangskoeffizient Konvektion \(W/(m^{2}*K)\)
- \(h_r\) Warmeiibergangskoeffizient Strahlung \(W/(m^{2}*K)\)
- \(\theta_s\) Oberflaichentemperatur \(°C\)
- \(\theta_a\) Lufttemperatur \(°C\)
- \(\theta_r\) Strahlungstemperatur \(°C\)
Die beiden Wärmeübergangkoeffizienten Konvektion und Strahlung können zu einem kombinierten Wärmeübergangskoeffizienten \(h = h_c + h_r\) zusammengefasst werden. Die Formel zur Bestimmung der Wärmestromdichte einer Oberfläche zu seiner Umgebung vereinfacht sich durch die Verwendung der Umgebungstemperatur θn zur Formel A2.2:
A2.2 Wärmestromdichte mittels Umgebungstemperatur¶
\(q= h * (\theta_s - \theta_n)\)
- \(h\) kombinierter Warmetibergangskoeffizient \(W/(m^{2}*K)\)
- \(\theta_n\) Umgebungstemperatur \(°C\)
Die Umgebungstemperatur θn wird gemäss Formel A2.3 ermittelt und kann als eine Gewichtung der Luft- und Strahlungstemperatur betrachtet werden.
A2.3 Umgebungstemperatur θn¶
\(\theta_n = \frac{h_c * \theta_a + h_r * \theta_r}{h_c + h_r} = F_c * \theta_a + (1- F_c) * \theta_r\)
- \(F_c\) = konvektiver Anteil
- \(F_c\) = \(h_c/(h_c+h_r)\)
A2.4 Umgebungstemperatur aussen, der Aussentemperatur θe:¶
\(\theta_e = \frac{h_c * \theta_{a,e} + h_{r,e} * \theta_{r,e}}{h_{c,e} + h_{r,e}}\)
A2.5 Umgebungstemperatur innen, der Raumtemperatur θi:¶
\(\theta_i = \frac{h_{c,i} * \theta_{a,i} + h_{r,i} * \theta_{r,i}}{h_{c,i} + h_{r,i}}\)
A2.6 Wärmeübergangswiderstände \(R_{se}\)¶
\(R_{se} = \frac{1}{h_c} = \frac{1}{h_{r,e} + h_{c,e}}\)
\(R_{se} = \frac{1}{\varepsilon * 4 * \sigma * T^{3}_{me} + (a + b * v)}\)
A2.7 Wärmeübergangswiderstände \(R_{si}\)¶
\(R_{si} = \frac{1}{h_i} = \frac{1}{h_{r,i} + h_{c,i}}\)
\(R_{si} = \frac{1}{\varepsilon * 4 * \sigma * T^{3}_{mi} + c * \sqrt[3]{\Delta \theta }}\)
- \(R_{se}\) Warmeiibergangswiderstand aussen \((m^{2}*K)/W\)
- \(R_{si}\) Warmeiibergangswiderstand innen \((m^{2}*K)/W\)
- \(\Delta \theta\) Temperaturdifferenz \(\Delta \theta = \theta_{si} - \theta_{a,i}\) \(K\)
- \(T_{me}\) Mitteltemperatur aussen \((T_{r,e}+T_{se})/2\) \(K\)
- \(T_{mi}\) Mitteltemperatur innen \((T_{r,e} + T_{si}) /2\) \(K\)
- \(a\) Regressionskoeffizient a = 4.0 \(W/(m^{2}*K)\)
- \(b\) Regressionskoeffizient b = 4.0 \((W*s)/(m^{3}*K)\)
- \(v\) Windgeschwindigkeit \(m/s\)
- \(c\) Regressionskoeffizient c = 1.31 (bei Warmestr6mung horizontal) \(W/(m^{2}*K^{4/3})\)
2.2 Wärmespeicherung¶
A2.8 statische, flächenbezogene Wärmespeicherfähigkeit¶
\(k_{stat} = \sum d_j*\rho_j*c_j\)
- \(d_j\) Dicke der Schicht j
- \(\rho_j\) Rohdichte der Schicht j
- \(c_j\) spezifische Warmekapazitat der Schicht j
A2.9 speicherwirksame Dicke \(d_{T,max}\)¶
\(d_{T,max} = \sqrt{\frac{a*T}{2*\pi}} = \sqrt{\frac{\lambda * T}{\rho*c*2*\pi}}\)
- \(a\) Temperaturleitfahigkeit \(m^{2}*s^{-1}\)
- \(T\) Periodenlange \(s\)
- \(\lambda\) Warmeleitfahigkeit \(W*(m*K)^{-1}\)
- \(\rho\) Rohdichte \(kg*m^{-3}\)
- \(c\) spezifische Warmekapazitat \(kJ*(kg*K)^{-1}\)
2.3 Wärmebrücken¶
A2.10 thermische Gesamtleitwert \(L_{i,j}\)¶
\(L_{3D,i,j} = \sum^{N_k}_{k=1}U_{k,(i,j)} * A_k + \sum^{N_m}_{m=1} \psi_{m(i,j)}*l_m + \sum^{N_n}_{n=1} \chi_{n(i,j)}\)
- \(L_{3D,i,j}\) thermischer Leitwert aus einer 3D-Berechnung \(W*K^{-1}\)
- \(U_{k,(i,j)}\) Warmedurchgangskoeffizient des 1D-Bauteils \(W*(m^{2}*K)^{-1}\)
- \(A_k\) Flache, über die der \(U_k\)-Wert gilt \(m^{2}\)
- \(\psi_{m(i,j)}\) längenbezogener Warmedurchgangskoeffizient \(W\)
- \(l_m\) Länge, über die der \(U_k\)-Wert gilt \(m\)
- \(X_{n,(i,j)}\) punktbezogener Warmedurchgangskoeffizient \(W*K^{-1}\)
- \(N_k\) Anzahl der Warmedurchgangskoeffizienten \(-\)
- \(N_m\) Anzahl der langenbezogenen Warmedurchgangskoeffizienten \(-\)
- \(N_n\) Anzahl der punktbezogenen Warmedurchgangskoeffizienten \(-\)
A2.11 Wärmebrückenzuschläge 2D¶
\(\psi = L_{2D} - \sum^{N_k}_{k=1}U_k*l_k\)
- \(L_{2D}\) thermischer Leitwert aus einer 2D-Berechnung \(W*(m*K)^{-1}\)
- \(U_k\) Warmedurchgangskoeffizient des 1D-Bauteils \(W*(m^{2}*K)^{-1}\)
- \(l_k\) Lange, über die der \(U_k\)-Wert gilt \(m\)
A2.12 Wärmebrückenzuschläge 3D¶
\(\chi = L_{3D} - \sum^{N_k}_{k=1}U_k*A_k - \sum^{N_m}_{m=1} \psi_m*l_m\)
- \(L_{3D}\) thermischer Leitwert aus einer 3D-Berechnung \(W*K^{-1}\)
- \(U_k\) Warmedurchgangskoeffizient des 1D-Bauteils \(W*(m^{2}*K)^{-1}\)
- \(A_k\) Flache, über die der \(U_k\)-Wert gilt \(m^{2}\)
- \(\psi_m\) langenbezogener Warme- durchgangskoeffizient \(W*(m*K)^{-1}\)
- \(l_m\) L$nge, über die der \(U_k\)-Wert gilt \(m\)
A2.13 Mittlerer U-Wert¶
\(U_m = \frac{L_{}i,j}{A_{tot}}\)
- \(L_{i,j}\) Gesamtleitwert aller betrachteten Gebaudehiillenbereiche \(W*K^{-1}\)
- \(A_{tot}\) Gesamtfliche der betrachteten Gebiudehiillenbereiche (Projektionsflaiche) \(m^{2}\)
3 Feuchte¶
3.1 Oberflächentemperatur¶
Die innere Oberflächentemperatur \(\theta_{si}\) einer Wand wird nach Formel A3.1 berechnet:
\(\theta_{si} = \theta_i - (R_{si} * U) * (\theta_i - \theta_e)\)
- \(\theta_e\) Aussentemperatur \(°C\)
- \(\theta_i\) Innentemperatur \(°C\)
- \(R_{si}\) Warmeiibergangswiderstand innen \(m^{2}*K*W^{-1}\)
- \(U\) Warmedurchgangskoeffizient der Wand \(W*(m^{2}*K)^{-1}\)
"""
Rsi:
windows, doors = 0.13 [m^2*K/W]
other = 0.25 [m^2*K/W]
"""
def surface_temperature(temp_out, temp_in, thermal_res_in, heat_transfer_coeff):
return temp_in - (thermal_res_in * heat_transfer_coeff) * (temp_in - temp_out)
def surface_temperature_from_factor(
temp_out,
temp_in,
surface_temp_factor,
):
return temp_out + surface_temp_factor * (temp_in - temp_out)
def surface_temperature_unheated(g1, temp_1, g2, temp_2, g3, temp_3):
"""g1 + g2 + g3 = 1"""
return (g1 * temp_1) + (g2 * temp_2) + (g3 * temp_3)
(
surface_temperature(-10, 21, 0.13, 0.2),
surface_temperature_from_factor(-10, 21, 0.974),
)
Out:
(20.194, 20.194)
Oberflächentemperaturfaktor¶
Oberflächentemperaturfaktor fRsi. Er ist als Verhältnis zwischen der Differenz der inneren Oberflächentemperatur eines Aussenbauteils und der Lufttemperatur aussen sowie der Differenz zwischen den Lufttemperaturen innen und aussen, bei vorgegebenem innerem Wärmeübergangswiderstand Rsi, definiert (siehe Formel A3.2).
Für flächige Bauteile (eindimensionale Wärmestromsituation) gilt: fRsi = 1 – (Rsi . U)
def surface_temperature_factor(surface_temperature, temp_out, temp_in):
return (surface_temperature - temp_out) / (temp_in - temp_out)
def simple_surface_temperature_factor(thermal_res_in, heat_transfer_coeff):
return 1 - (thermal_res_in * heat_transfer_coeff)
(
surface_temperature_factor(20.194, -10, 21),
simple_surface_temperature_factor(0.13, 0.2),
)
Out:
(0.974, 0.974)
Feuchtebelastung¶
Die Feuchtebelastung in einem Raum ist abhängig von der Feuchteproduktion G, der Aussenluftfeuchte νe und dem Aussenluft-Volumenstrom qv. Der raumseitige Feuchteüberschuss ∆ν kann gemäss Formel A3.5 bestimmt werden.
In Tabelle A3.2 ist die Feuchteproduktion G einer Person in Abhängigkeit zu seiner Tätigkeit angegeben.
(A3.5)
\(\Delta v = v_i - v_e = \frac{G}{q_v}\)
- \(\Delta v\) raumseitiger Feuchtetiberschuss \(g*m^{-3}\)
- \(v_i\) volumenbezogene Raumluftfeuchte \(g*m^{-3}\)
- \(v_e\) volumenbezogene Aussenluftfeuchte \(g*m^{-3}\)
- \(G\) Feuchteproduktion im Raum \(g*h^{-1}\)
- \(q_v\) Aussenluft- Volumenstrom \(m^{3}/h\)
| Tatigkeit | Feuchteproduktion G in \(g/h\) |
|---|---|
| ruhig liegend, schlafend | 45 |
| ruhig sitzend | 60 |
| sitzende Tatigkeit (Biro, Schule, Labor), ruhig stehend | 70 |
| leichte Tatigkeit, stehend (Laden, Werkbankarbeit, Labor) | 95 |
| mittelschwere Tatigkeit, stehend (Haushalt, Werkstatt) | 115 |
Tabelle: SIA 180:2014[3.2]
A3.5
def excess_humidity_room(indoor_hum, outdoor_hum):
return indoor_hum - outdoor_hum
def excess_humidity_room_from_flow(hum_production_person, outdoor_air_flow):
return hum_production_person / outdoor_air_flow
# A3.6
def water_vapour_overpressure(excess_humidity_room, temp_in):
RV = 462 # Pa*m3 * (kg*K)^-1
temp_in += 273.15
return excess_humidity_room * RV * temp_in
# A3.7
def water_vapour_pressure_in(water_vapour_overpressure, water_vapour_pressure_out):
return water_vapour_overpressure + water_vapour_pressure_out
3.6 Wasserdampfüberdruck¶
Der raumseitige Wasserdampfüberdruck ∆p im Raum lässt sich somit nach Formel A3.6, der raumseitige Wasserdampfdruck pv,i nach Formel A3.7 ermitteln:
(A3.6)
\(\Delta p = \Delta v * R_v * T_i\)
(A3.7)
\(P_{v,i} = P_{v,e} + \Delta p\)
- \(p_{v,i}\) Wasserdampfdruck innen \(Pa\)
- \(p_{v,e}\) Wasserdampfdruck aussen \(Pa\)
- \(\Delta_{P}\) raumseitiger Wasserdampfüberdruck \(Pa\)
- \(R_v\) spez. Gaskonstante für Wasserdampf = 462 \(Pa * m^{3} * (kg*K)^{-1}\)
- \(T_i\) absolute Temperatur innen \(K\)
Für maritime Klimate wird im Anhang A.2 die Luftfeuchtelast in fünf Luftfeuchteklassen gemäss Tabelle A3.3 eingeteilt und jeder Klasse in Abbildung A3.4 ein Wert für den raumseitigen Feuchteüberschuss ∆ν bzw. den raumseitigen Wasserdampfüberdruck ∆p in Abhängigkeit des monatlichen Mittelwerts der Aussenlufttemperatur zugeordnet.
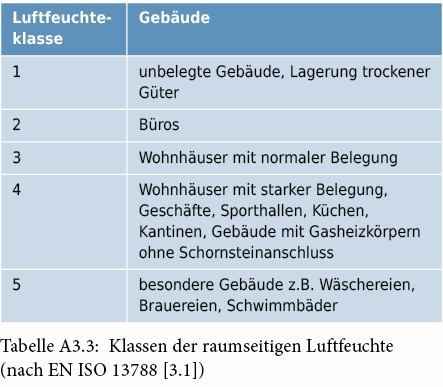
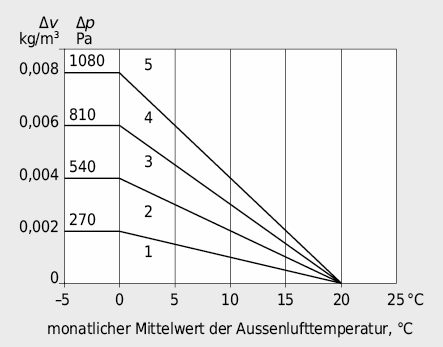
Abbildung A3.4: Raumseitige Luftfeuchteklassen in Abhängigkeit der Aussenlufttemperatur (EN ISO 13788 [3.1])
Raumseitige Randbedingungen nach SIA 180 [3.2]¶
Um Feuchteschäden zu vermeiden, darf die Feuchte in Räumen mit Personenbelegung die in Tabelle A3.4 angegebenen Werte im Tagesmittel in Abhängigkeit zur Aussenlufttemperatur nicht übersteigen. Die Angaben zur relativen Luftfeuchte beziehen sich auf eine Raumlufttemperatur von 20 °C und ein fRsi von 0,70. Für abweichende Raum- und Aussenlufttemperaturen ist die maximal zulässige relative Feuchte in Abbildung A3.5 angegeben, berechnet mit Formel A3.8. Die Aussenluft-Volumenströme sind so zu wählen, dass diese Grenzen nicht überschritten werden.
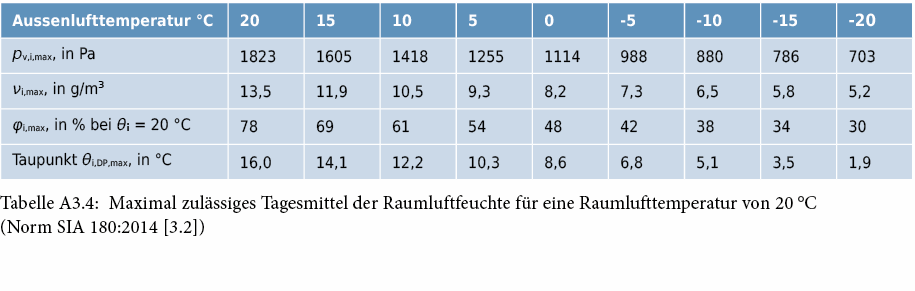
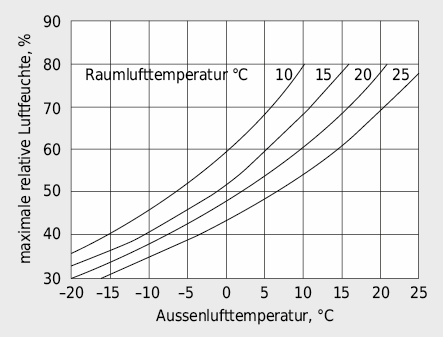
Abbildung A3.5: Maximal zulässige relative Feuchte der Raumluft (Tagesmittelwerte) (Norm SIA 180:2014 [3.2])
Bei abweichenden Nutzungsbedingungen (Raumlufttemperaturen ≠ 20 °C) und in Räumen mit unvermeidbaren Wärmebrücken mit einem Oberflächentemperaturfaktor unter 0,70 ist eine Berechnung der maximal zulässigen relativen Raumluftfeuchte φi,max mit der Gleichung A3.8 notwendig:
(A3.8)



4 Luftströmungen¶
A4.1 Rechtecköffnung¶
\(q_{v,Rechtecköffnung} = c_d * H * B * \frac{1}{3}*\sqrt{g*H*\frac{(T_i-T_e)}{T_e}}\)
Die empirische Grösse cd ist insbesondere von der Fensterposition und -geometrie abhängig [4.2] und kann – falls keine Resultate aus Experimenten oder CFD-Simulationen vorliegen – in grober Näherung mit etwa 0.6 angenommen werden.
A4.2 Kippfenstern¶
\(q_{v,Kippflügel}(\alpha) = c_k(\alpha) * q_{v,Rechtecköffnung}\)
5 Lichttechnik¶

5.1 Lichtstrom Tagsehen¶
\(\Phi_v = Km * \int_{380nm}^{780nm} \Phi_{e\lambda}(\lambda) * V(\lambda) d\lambda\)
5.2 Lichstrom Nachtsehen¶
\(\Phi'_v = K'm * \int_{380nm}^{780nm} \Phi_{e\lambda}(\lambda) * V'(\lambda) d\lambda\)
5.3 Skalierungsfaktoren Km¶
\(K_m \approx 683 lm/W\)
\(K'_m \approx 1700 lm/W\)
5.4 Lichtstärke¶
\(\Phi_v(\varphi_1) = lv(\varphi_1)* \Omega\)
5.5 Lichtstärke¶
\(l_v(\varphi_1) = \frac{d\Phi_v(\varphi_1)}{d\Omega}\)
Iv (φ1) wird als Lichtstärke bezeichnet. Die physiologische Einheit Candela (cd) der Lichtstärke Iv ist zugleich eine Basiseinheit des SI-Einheitensystems. Der Gesamtlichtstrom Φv, tot berechnet sich aus:
5.6 Gesamtlichtstrom Φv, to¶
\(\Phi_{v,tot} = \int_{4\pi} l_v (\varphi_1) * d\Omega\)
5.7 Leuchtdichte¶
\(L_{v0} = \frac{l_v(\varphi = 0)}{A}\)
\(L_{v(\varphi1)} = \frac{l_v (\varphi_1)}{A*\cos \varphi_1} * \frac{1}{\cos \varphi_1}\)
\(L_{v(\varphi1)} = \frac{dl_v}{dA} * \frac{1}{\cos \varphi_1}\)
| Leuchtdiode | Lichstrom, lm |
|---|---|
| Leuchdiode | 10 \(^{-2}\) |
| LED-Lampe 220 V, 8 W | 480 |
| Gluhlampe 220 V, 60 W | 730 |
| Gluhlampe 220 V, 100 W | 1380 |
| Leuchtstoffrohre 220 V, 40 W | 2300 |
| Quecksilberdampflampe 220 V, 125W | 5400 |
| Lichtbogen 250 W | \(\sim\) 10'000 |
| Quecksilberdampflampe 220 V, 2000 W | \(\sim\) 125'000 |
| Xe-Hochstdrucklampe 100 kW | 3*10 \(^{6}\) |
Tabelle 5.1: Gesamtlichtstrom einiger Lichtquellen
5.8 Leuchtdichte¶
| \(cd*m^{-2}\) | \(cd*m^{-2}\) |
|---|---|
| Nachthimmel 10 \(^{-3}\) | Glimmlampe 2+10 \(^2\) - 1 * 10 \(^3\) |
| graue Wolken 10 \(^{3}\) | Leuchtstofflampe 3*10 \(^3\) - 7 * 10 \(^3\) |
| blauer Himmel 3*10 \(^{3}\) | Glühlampe 3*10 \(^4\) - 3 * 10 \(^5\) |
| weisse Wolken 10 \(^{4}\) | Bogenlampe 1.8 * 10 \(^8\) |
| Vollmond 2.5 * 10 \(^{3}\) | Hg-Höchstdrucklampe 6 - 10 \(^8\) |
| Sonne 1.5 * 10 \(^{9}\) | Xe-Höchstdrucklampe 1 * 10 \(^{10}\) |
Tabelle 5.2: Leuchdichten ausgewählter Lichtquellen
5.9 Beleuchtungsstärke¶
\(E_v = \frac{\Phi_v}{A_E}\)
\(E_v = \frac{d\Phi_v}{dA_E}\)
TODO: Bild
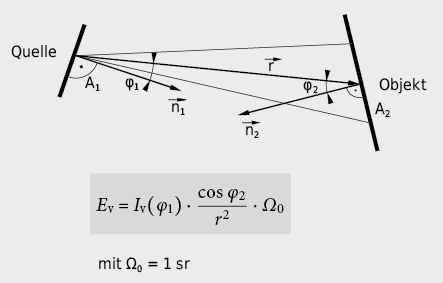
\(E_v = l_v(\varphi_1) * \frac{\cos \varphi_2}{r^2} * \Omega_0\)
| Beluchtungsstärke | zeitpunkt | lx |
|---|---|---|
| Sonnenlicht | Juni Dezember |
bis 100'000 9'000 |
| Tageslicht bei bedecktem Himmel | Juni Dezember |
4'000 - 20'000 900 - 2'000 |
| Vollmond | 0.25 | |
| Sterne ohne Mond, klare Nacht | 10 \(^{-3}\) | |
| Grenze der Farbwahrnehmung | 3 | |
| Arbeitsplatzbeleuchtung, hohe Ansprüche | 1'000 | |
| Wohnzimmerbeleuchtung | 120 |
Tabelle: Beleuchtungsstärke
Gegenüberstellung von physikalischen und photometrischen Strahlungsgrössen¶
6 Energie/Leistung¶
A6.1 Klimakorrektur mit akkumulierten Temperaturdifferenzen (ATD)¶
6.2 Heizenergiebedarf¶
\(E_{H,an} = \frac{\theta_{\sum,an}}{\theta_{\sum,per}}*E_{H,per}\)
6.3 Heizenergiebedarf¶
\(E_{H,1} = \frac{\theta_{\sum,per1}}{\theta_{\sum,per2}}*E_{H,2}\)
A6.4 Statische Wärmekapazität \(C_{stat}\)¶
\(C_{stat} = \sum A_i * \sum d_j * \rho_j * c_j\)
- \(A_i\) Flache des Bautells \(m^{2}\)
- \(d_j\) Dicke der Schicht j \(m\)
- \(\psi_j\) Rohdichte der Schicht j \(kg*m^{3}\)
- \(c_j\) spezifische Warmekapazitat der Schicht \(kJ*(kg*K)^{-1}\)
A6.5 Dynamische Wärmekapazität \(C_{stat}\)¶
6.5 Kühlungsbedarf¶
A6.6 Kühlungsbedarf¶
\(C_r = \sum A_i*k_i\)
- \(A_i\) Flache des Bauteils i \(m^{2}\)
- \(K_i\) flachenbezogene Warmespeicherfahigkeit des Bauteils (mit \(R_{si}\) und \(R_{se}\)),
berechnet nach EN ISO 13786 [6.7] \(kJ * (m^{2}* K)^{-1}\)
Anhang¶
9.2 maximal zulässigen U-Wertes¶
9.3 maximal zulässigen U-Wertes bei max zul. Luftgeschwindigkeit¶
9.4 Sonnenschutz Gesamtenergiedurchlassgrad des Fensters¶
Total running time of the script: ( 0 minutes 0.001 seconds)
Download Python source code: plot_1_Bauphysik.py